Система координат в геодезии, в топографии, в картографии © Геостарт

В геодезии все координаты могут быть представлены в виде двух групп

• Прямоугольники.
• Полюса.

Обе группы можно рассматривать как уровневые (двумерные) и пространственные (трехмерные) системы.

Прямоугольные системы Прямоугольные системы включают цилиндрические отображения Гаусса-Крюгера, индивидуальные системы отсчета и местные системы координат.

Полярная система включает географическую, астрономическую и геодезическую динамику, центр Земли и систему топоцентров.

Географическая система координат

Замкнутая поверхность внешних контуров Земли представлена сферической геометрией. Носовая часть сферической поверхности может рассматриваться как основное направление ориентации. В упрощенном представлении уменьшенной модели планеты в виде сферы (форма Земли) визуально видны приемлемые опорные линии в виде Гринвичского меридиана и экваториальных линий.

Этот пример представляет собой глобальную приемлемую пространственную систему географических координат. Вводятся понятия географической длины и широты. Это молекулярные единицы и представляют собой угловые величины.

Многие знакомы с их определениями. Напомним, что продольная протяженность конкретной точки представляет собой угол между нулевым (гринвичским) меридианом и двумя уровнями, проходящими через один меридиан в данной точке местоположения. Широта точки — это угол, образованный между уровнем весов (или нормалью) и экватором в ней.

Понятия астрономической и геодезической системы координат и их различия

Географические системы условно объединяют астрономическую и геодезическую системы. Чтобы прояснить различия, следует обратить внимание на определение геодезических и астрономических координат (широта, широта и высота). В астрономических системах широта принимается как угол между экваториальным уровнем и шпуром в точке определения.

Тогда форма Земли в ней считается условным геоидом, который математически приближается к сфере. В геодезических системах широта образуется вертикалью на поверхности наивного эллипсоида в определенной точке и экваториальным уровнем. Третья координата этих систем дает решающее представление об их различиях.

Астрономическая (ортометрическая) высота — это высота по бобу между точками на поверхности плоского геоида. Геодезическая высота — это расстояние по вертикали от поверхности эллипсоида до расчетной точки.

Система плоских прямоугольных систем координат Гаусса-Крюгера

Каждая система координат имеет свое теоретическое научное и практическое экономическое применение, как глобальное, так и региональное. В особых случаях в системах отсчета могут использоваться местные и условные системы координат, которые могут быть объединены путем математических расчетов и вычислений.

Геодезическая прямоугольная система уровней представляет собой проекцию отдельных шестиугольных зон эллипсоида. Регистрируя эту геометрию в горизонтально выровненном цилиндре, каждая зона появляется индивидуально на внутренней внутренней поверхности. Эти сферические зоны примыкают к меридиану с шагом 6 градусов.

При развертывании на нивелире проекция выполняется по разработанному немецким ученым Гауссу Крюгеру. Таким образом, углы между всеми направлениями сохраняют свою цену. Поэтому ее также называют изогенной.

Ось абсцисс в зоне проходит через условную ось меридиана (ось х) и через продольный координатный вал по линии экватора (ось осей). Длина линии по меридиану оси передается по линии экватора без деформации и с деформацией на краю зоны.

Геоцентрические и топоцентрические системы координат

Спутниковые координаты земля-центр частично основаны на том же полярном законе, с той лишь разницей, что главные оси в трехмерном пространстве (x, y, g) имеют разное происхождение и ориентацию. В землецентрической системе началом является центр масс Земли; ось x ориентирована вдоль Гринвичского меридиана на Эквадор; ось y находится в прямоугольном положении к востоку от x; ось z изначально имеет полярную ориентацию вдоль вторичной оси эллипсоида; ось g имеет полярную ориентацию вдоль вторичной оси эллипсоида. Его координаты следующие.

• На уровне Эквадора — непосредственное восхождение земного центра спутника.
• На уровне меридиана — отклонение земного центра спутника
• Радиальное отклонение центра тяжести Земли — это расстояние от центра тяжести Земли до спутника.

При наблюдении за движением спутника из устойчивой точки Земли используется система верхнего центра в координатах, параллельных оси геоцентрической системы, начальная точка которой считается точкой наблюдения. Координаты такой системы:.

• Спутниковая прямая система мгновенного восхождения
• Дивергенция спутника
• Радиус спутника лучи спутника
• Центрированный на Земле вектор радиусов в точке наблюдения.

Современный спутниковый мир WGS-84, PZ-90 Глобальная система отсчета включает не только координаты, но и другие параметры и характеристики, важные для геодезических измерений, наблюдений и навигации. К ним относятся геодезические и другие константы.

Абсцисса, ордината, начало координат и единичный отрезок

Эти оси имеют общее название. В частности, горизонтальная ось называется осью абсцисс и записывается как $ ox $.

Вертикальная ось называется осью ординат и пишется $ u $.

Поскольку оси пересекают друг друга перпендикулярно и вертикально, такая система координат называется прямоугольником.

Точка пересечения координат является началом. Эта точка обычно называется $ o $ и обозначается как точка отсчета. Иногда ее также называют нулевой точкой.

Каждая ось выбирает единичный отрезок, который может быть использован для вычисления координат объекта. Длина единичного отрезка может быть любой, но должна быть одинаковой на каждой оси. Другими словами, если единичный отрезок оси абсцисс равен, например, 1 см, то единичный отрезок ординат также должен быть равен 1 сантиметру.

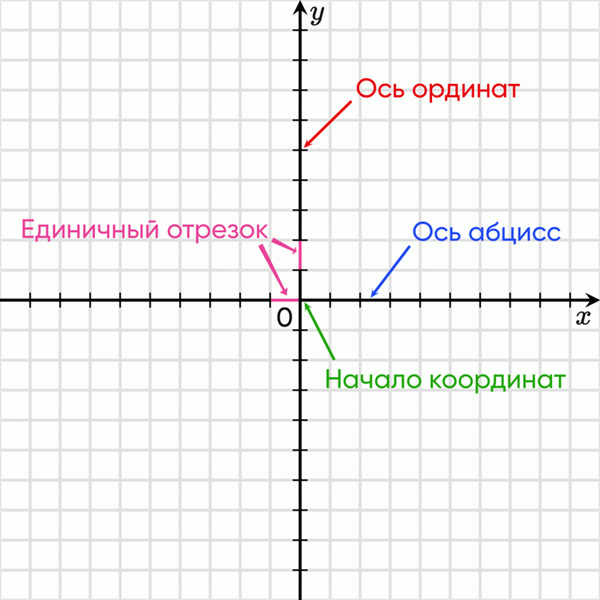
АККИ, право, начало и единичный отрезок

Положительное и отрицательное направление

Ось $ имеет стрелку, направленную в положительную сторону.

• Таким образом, ось $ ox $ обычно имеет положительное направление вправо.
• Ось $ ou $ имеет положительное направление снизу вверх.

В этом случае часть прямой $ ox $ слева от $ ou $ получает отрицательную цену. Аналогично, часть прямой $ ou $ ниже $ o $ также получает отрицательную цену.

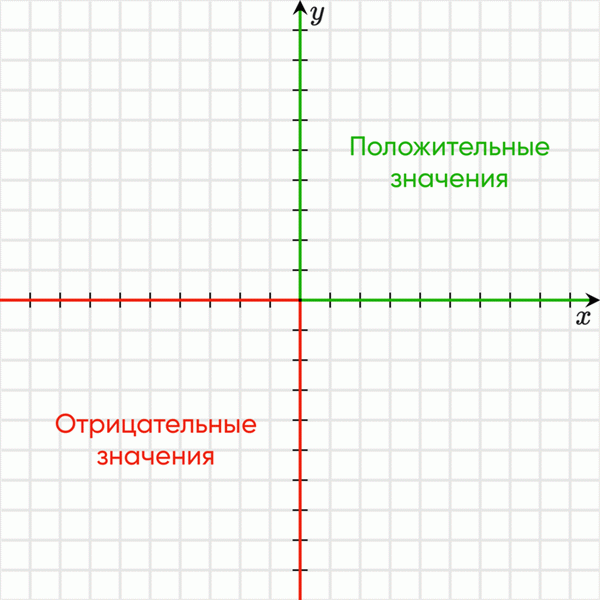
Таким образом, в совокупности

• Принцип координат $ o $.
• Она пересекается под правильным углом с заданным направлением и $ oh $ и $ ou $.
• Конкретные единичные отрезки

Они образуют прямоугольную систему математических координат, плоскости называются уровнями координат.

Или другими словами:.

Прямоугольная система координат — это два перпендикуляра к координатам с заданным направлением, единицей длины и точкой отсчета ее разреза.

В письменной форме система координат называется $ оху $.

Четверти

Координатная ось делит уровень на четыре части. Они характеризуются латинским номером. Каждая часть называется «квадрантом». Другие названия — «координатные углы» или «квадранты». Квадранты отсчитываются против часовой стрелки в порядке, показанном на диаграмме ниже.

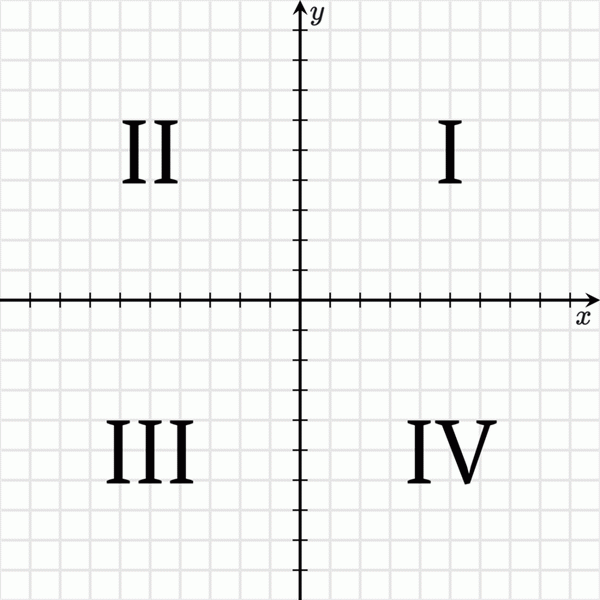
Квадрант уровня координат

В квадранте I цены $ x $ и $ y $ положительны. Если координаты объектов $ x $ и $ y $ положительны, то он оказывается квартальным.

В квадранте II координаты $ y $ положительны, а $ x $ отрицательны.

В III квартале и $ x $, и $ y $ имеют отрицательные цены.

В IV квартале $ x $ имеет положительную цену, а $ y $ — отрицательную.

Немного из истории

В латинском языке слово «координаты» происходит от двух других слов: «вместе», «расположенный» и «устроенный».

Необходимость найти координаты объекта впервые появилась в географии и астрономии. Широта и широта использовались для определения положения точек на поверхности небесной сферы или планеты.

Таким образом, вычислять координаты точек начали еще в 14 веке. Однако именно французский математик по имени Рене Декарт в 17 веке рационализировал и систематизировал все знания. Поэтому прямоугольную систему координат также называют «декартовой».

I Система координат на прямой

Чтобы определить СК как прямую линию, достаточно преобразовать ее в числовую ось. Для этого нужно выбрать одно направление и две точки. Координатами точки А является действительное числовое значение x, представляющее точку a:x =±d (a, 0).

Тот факт, что точка A имеет координату x, описывается формой a(x). Расстояние между точками a₁(х₁) и а₂(х₂) вычисляется по типу

II Декартова прямоугольная система координат на плоскости

Он определяется двумя взаимными вертикальными арифметическими осями с общим принципом, равным единичному отрезку, определяющим, кто считается первым, а кто вторым.

Общий принцип называется принципом координат и обозначается O. Оси называются координатными валами или координатами. Первая из них называется осью вершины и символизируется символом OH, а ось второй координаты — символом o.

Даже в любой точке уровня. Давайте спроецируем ее на координатные оси. Другими словами, проведем вертикали от m к o и oy. Основание этих перпендикуляров обозначим через m₁и M₂соответственно. Каждая из этих точек определяет свои координаты на своей оси.₁(х) и m₂(u).

Число х называется передней осью точки m, а у — прямой линией точки M.

То, что координаты x и y записаны на точках на уровне M

Форма m (x, y).

Расстояние между точками a₁(х₁, a₁) и a₂(х₂, a₂) вычисляется по типу

.

Каждая ось делит плоскость на две полуоси: верхнюю и нижнюю (ω-ось), правую и левую (ω-ось).Две оси делят уровень на четыре четверти. Цифры и обозначения координат показаны на схеме

III дпск в пространстве

Они определяются тремя вертикалями между арифметическими осями, которые имеют общий принцип и одинаковые единичные отрезки. Оси пронумерованы в определенном порядке. То есть указывается, какая считается первой, какая второй, а какая третьей.

Первая и вторая называются так же, как и в предыдущем пункте, а третья называется осью приложения и обозначается буквой O.

Каждая пара осей определяет плоскость, называемую уровнем координат. Они обозначаются xou, xo z и yo z. Каждый уровень делит пространство на два места. В частности, горизонтальный уровень XOU делится на высший (расположенный в положительном направлении оси OZ)

низший полувнешний.

Даже в любой пространственной точке. спроецируем на уровень Xou. Возьмем точку m₁на этом уровне, где координаты x и y четко определены. Эти координаты называются точками абсцисс и точкой m. Третья координата, соответствующая точке m, задается видом

z =±d(m, m)₁),

где знак «+» выбирается, если точка M расположена в верхней полуокружности

m (расстояние между точками x₁, a₁, z₁) и n(x₂, a₂, z₂) вычисляется по типу

.

Если c (x, y, z) делит заданный участок mn как λ

(т.е. MC: C n =λ), то

.

Если требуется найти координаты среды mn-сечения, то достаточно на этих типах поставить λ = 1.

История

Прямоугольная система координат была впервые введена Рене Декартом в рассуждениях Пьера Ферма, но его работа была опубликована только после его смерти; Декарт и Фермат применили метод координат только к уровням; прямоугольная система координат была введена Пьером Ферматом в его рассуждениях о работе метода.

Метод трехмерных координат был впервые реализован Леонгардом Эйлером еще в XVIII веке.

bg:Καρτεσιανό σύστημα συντεταγμένων el:Καρτεσιανό σύστημα συντεταγμένων fa:دستگاه مختصات دکارتی he:מערכת צירים קרטזית hi:कार्तीय निर्देशांक पद्धत id:Sistem koordinat Kartesius is: Kartesíusarhnitakerfið pl:Układ współrzędnych kartezjańskich sq:Sistemi koordinativ kartezian sr: Καρτεσιανά συστήματα συντεταγμένων sv: TA:. காட்டீசியன்முறைமைமுைறமை Великобритания: Декартова система координат

Прямоугольная система координат в трехмерном пространстве

Аналогичная система существует в трехмерном евклидовом пространстве, но она состоит не из двух, а только из трех осей O x , O y и O z. Это три взаимно перпендикулярные линии, где O z называется осью перпендикуляров.

Направление координатных осей разделяет левую и правую декартовы системы координат в трехмерном пространстве.

Координатные оси пересекаются в точке O, называемой началом координат. Каждая ось имеет положительное направление, обозначенное стрелкой на оси: если ось O x повернута на 90° против часовой стрелки и ее положительное направление совпадает с направлением оси O y, то это относится и к положительному направлению оси O z. Такая система считается вращающейся по часовой стрелке.

То есть, если направление x сравнивается с большим пальцем руки, то указательный палец отвечает за y, а средний — за z.

Аналогично формируется левая система координат. Эти две системы не могут быть совмещены, так как их соответствующие оси не совпадают.